Laws, Sausages and ConvNets
Laws, like sausages, cease to inspire respect in proportion as we know how they are made.
Convolutional Neural Networks (CNNs or ConvNets in short) give the state-of-the-art results in many problem domains. Nowadays, using them is simpler than ever: pretty much all the frameworks out there (Theano, Torch, Caffe…) support them out-of-the-box. If you care only about applying such networks - move along then, there’s nothing to see here. This post is about the nuts and bolts: algorithms, implementations and optimizations. It is about how ConvNets are made.
Full-blown ConvNets may incorporate a variety of ideas and mechanisms, but in the following I’m going to focus on their very core: convolutional layers. Convolution is a simple mathematical operation, so the enormous complexity involved in implementing convolutional layers may be surprising. The fun begins due to the interaction of mathematical and algorithmic considerations with real-world constraints regarding parallelism, memory-hierarchies and heterogeneous systems. And then - to really get the party started - there’s the question of numerical accuracy.
This post is long and rich in details. Perhaps some snippets, worth
highlighting, will get dedicated short posts of their own in the future. Python
will be used for algorithmic prototyping. C and some C++, together
with OpenCL (which I prefer over CUDA),
will be used for implementations. Concurrency is going to get a lot of
attention, mostly in the context of heterogeneous computing (e.g. GPUs and
alike).
The general spirit of things to come is perhaps somewhat unorthodox within the deep-learning community. It is very common to introduce and think about convolutional layers in terms of neural connectivity and weights-sharing, e.g. as in this diagram (taken from here, and chosen for its aesthetic appeal):
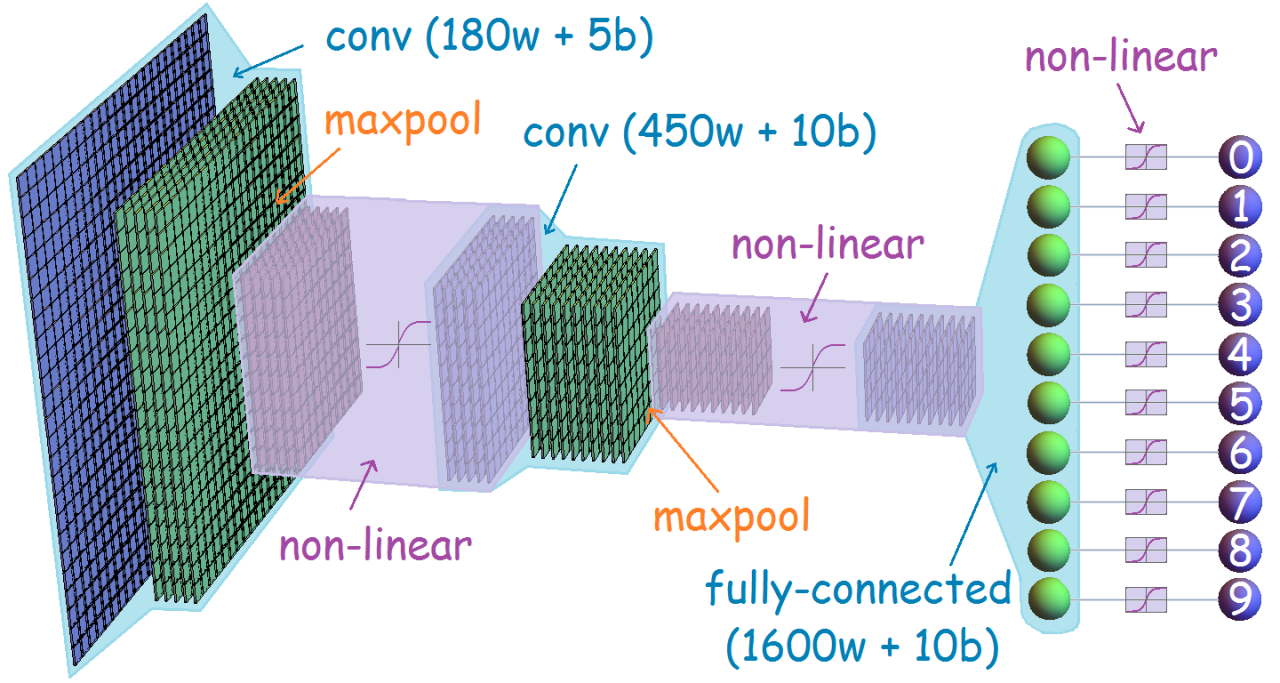
I personally think that weights-sharing is a horrible way to describe and understand CNNs, and it really misses the point of what backpropagation is all about: automatic differentiation of real-valued functions. Instead of dealing with networks, I take the point of view that a convolutional layer is simply a differentiable function. There’s more to it than that, of course: backpropagation is a modular reformulation of the chain rule, and the differentiable function that model a convolutional layer needs to be reformulated as a differentiable node. This will be explained in details.
While writing this overview, I discovered that writing is… well, hard. Proofreading, editing and phrasing are never-ending tasks, and as such, I’m not done with them. Some parts of this text are still rather crude, and I will likely continue to edit it long after its publication. Corrections, suggestions and notes are most welcomed!
Content
- Convolutions
- Feature Detectors
- Linear Convolution and Cross-Correlation
- The Discrete Fourier Transform
- Circular Convolution and Spectral Interpolation
- Backpropagation
- Convolutional Layers
- The Backward Algorithm
- Backpropagation in the Frequency Domain
- Concurrent Training
- Quasilinearity
- Cooley-Tukey and Good–Thomas
- Bluestein, Rader and Singleton
- Decimation in Time and Frequency
- Transpositions and Permutations
- Execution Plans
- Quasilinear Convolutions
- Overlap Methods
- Parallelized Filters
- Overlap-Discard
- Overlap-Add
- Convolution in Parts
- Multidimensionality
- Separability
- The Row-Column Method and The Helix Transform
- Image Memory Objects
- Shared-Memory Bank Conflicts